Starting from its - very - recent 2.1 release, TensorFlow supports what is called mixed-precision training (in the following: MPT) for Keras. In this post, we experiment with MPT and provide some background. Stated upfront: On a Tesla V100 GPU, our CNN-based experiment did not reveal substantial reductions in execution time. In a case like this, it is hard to decide whether to actually write a post or not. You could argue that just like in science, null results are results. Or, more practically: They open up a discussion that may lead to bug discovery, clarification of usage instructions, and further experimentation, among others.
In addition, the topic itself is interesting enough to deserve some background explanations – even if the results are not quite there yet.
So to start, let’s hear some context on MPT.
This is not just about saving memory
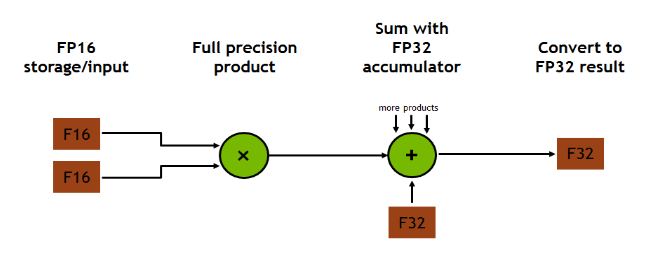
One way to describe MPT in TensorFlow could go like this: MPT lets you train models where the weights are of type float32 or float64, as usual (for reasons of numeric stability), but the data – the tensors pushed between operations – have lower precision, namely, 16bit (float16).
This sentence would probably do fine as a TLDR; 1 for the new-ish MPT documentation page, also available for R on the TensorFlow for R website. And based on this sentence, you might be lead to think “oh sure, so this is about saving memory”. Less memory usage would then imply you could run larger batch sizes without getting out-of-memory errors.
This is of course correct, and you’ll see it happening in the experimentation results. But it’s only part of the story. The other part is related to GPU architecture and parallel (not just parallel on-GPU, as we’ll see) computing.
AVX & co.
GPUs are all about parallelization. But for CPUs as well, the last ten years have seen important developments in architecture and instruction sets. SIMD (Single Instruction Multiple Data) operations perform one instruction over a bunch of data at once. For example, two 128-bit operands could hold two 64-bit integers each, and these could be added pairwise. Conceptually, this reminds of vector addition in R (it’s just an analogue though!):
Or, those operands could contain four 32-bit integers each, in which case we could symbolically write
With 16-bit integers, we could again double the number of elements operated upon:
Over the last decade, the major SIMD-related X-86 assembly language extensions have been AVX (Advanced Vector Extensions), AVX2, AVX-512, and FMA (more on FMA soon). Do any of these ring a bell?
Your CPU supports instructions that this TensorFlow binary was not compiled to use:
AVX2 FMAThis is a line you are likely to see if you are using a pre-built TensorFlow binary, as opposed to compiling from source. (Later, when reporting experimentation results, we will also indicate on-CPU execution times, to provide some context for the GPU execution times we’re interested in – and just for fun, we’ll also do a – very superficial – comparison between a TensorFlow binary installed from PyPi and one that was compiled manually.)
While all those AVXes are (basically) about an extension of vector processing to larger and larger data types, FMA is different, and it’s an interesting thing to know about in itself – for anyone doing signal processing or using neural networks.
Fused Multiply-Add (FMA)
Fused Multiply-Add is a type of multiply-accumulate operation. In multiply-accumulate, operands are multiplied and then added to accumulator keeping track of the running sum. If “fused”, the whole multiply-then-add operation is performed with a single rounding at the end (as opposed to rounding once after the multiplication, and then again after the addition). Usually, this results in higher accuracy.
For CPUs, FMA was introduced concurrently with AVX2. FMA can be performed on scalars or on vectors, “packed” in the way described in the previous paragraph.
Why did we say this was so interesting to data scientists? Well, a lot of operations – dot products, matrix multiplications, convolutions – involve multiplications followed by additions. “Matrix multiplication” here actually has us leave the realm of CPUs and jump to GPUs instead, because what MPT does is make use of the new-ish NVidia Tensor Cores that extend FMA from scalars/vectors to matrices.
Tensor Cores
As documented, MPT requires GPUs with compute capability >= 7.0. The respective GPUs, in addition to the usual Cuda Cores, have so called “Tensor Cores” that perform FMA on matrices:
The operation takes place on 4x4 matrices; multiplications happen on 16-bit operands while the final result could be 16-bit or 32-bit.
We can see how this is immediately relevant to the operations involved in deep learning; the details, however, are not necessarily clear.
Leaving those internals to the experts, we now proceed to the actual experiment.
Experiments
Dataset
With their 28x28px / 32x32px sized images, neither MNIST nor CIFAR seemed particularly suited to challenge the GPU. Instead, we chose Imagenette, the “little ImageNet” created by the fast.ai folks, consisting of 10 classes: tench, English springer, cassette player, chain saw, church, French horn, garbage truck, gas pump, golf ball, and parachute. 2 Here are a few examples, taken from the 320px version:

Figure 3: Examples of the 10 classes of Imagenette.
These images have been resized - keeping the aspect ratio - such that the larger dimension has length 320px. As part of preprocessing, we’ll further resize to 256x256px, to work with a nice power of 2. 3
The dataset may conveniently be obtained via using tfds, the R interface to TensorFlow Datasets.
library(keras)
# needs version 2.1
library(tensorflow)
library(tfdatasets)
# available from github: devtools::install_github("rstudio/tfds")
library(tfds)
# to use TensorFlow Datasets, we need the Python backend
# normally, just use tfds::install_tfds for this
# as of this writing though, we need a nightly build of TensorFlow Datasets
# envname should refer to whatever environment you run TensorFlow in
reticulate::py_install("tfds-nightly", envname = "r-reticulate")
# on first execution, this downloads the dataset
imagenette <- tfds_load("imagenette/320px")
# extract train and test parts
train <- imagenette$train
test <- imagenette$validation
# batch size for the initial run
batch_size <- 32
# 12895 is the number of items in the training set
buffer_size <- 12895/batch_size
# training dataset is resized, scaled to between 0 and 1,
# cached, shuffled, and divided into batches
train_dataset <- train %>%
dataset_map(function(record) {
record$image <- record$image %>%
tf$image$resize(size = c(256L, 256L)) %>%
tf$truediv(255)
record
}) %>%
dataset_cache() %>%
dataset_shuffle(buffer_size) %>%
dataset_batch(batch_size) %>%
dataset_map(unname)
# test dataset is resized, scaled to between 0 and 1, and divided into batches
test_dataset <- test %>%
dataset_map(function(record) {
record$image <- record$image %>%
tf$image$resize(size = c(256L, 256L)) %>%
tf$truediv(255)
record}) %>%
dataset_batch(batch_size) %>%
dataset_map(unname)In the above code, we cache the dataset after the resize and scale operations, as we want to minimize preprocessing time spent on the CPU.
Configuring MPT
Our experiment uses Keras fit – as opposed to a custom training loop –, and given these preconditions, running MPT is mostly a matter of adding three lines of code. (There is a small change to the model, as we’ll see in a moment.)4
We tell Keras to use the mixed_float16 Policy, and verify that the tensors have type float16 while the Variables (weights) still are of type float32:
# if you read this at a later time and get an error here,
# check out whether the location in the codebase has changed
mixed_precision <- tf$keras$mixed_precision$experimental
policy <- mixed_precision$Policy('mixed_float16')
mixed_precision$set_policy(policy)
# float16
policy$compute_dtype
# float32
policy$variable_dtypeThe model is a straightforward convnet, with numbers of filters being multiples of 8, as specified in the documentation. There is one thing to note though: For reasons of numerical stability, the actual output tensor of the model should be of type float32.
model <- keras_model_sequential() %>%
layer_conv_2d(filters = 32, kernel_size = 5, strides = 2, padding = "same", input_shape = c(256, 256, 3), activation = "relu") %>%
layer_batch_normalization() %>%
layer_conv_2d(filters = 64, kernel_size = 7, strides = 2, padding = "same", activation = "relu") %>%
layer_batch_normalization() %>%
layer_conv_2d(filters = 128, kernel_size = 11, strides = 2, padding = "same", activation = "relu") %>%
layer_batch_normalization() %>%
layer_global_average_pooling_2d() %>%
# separate logits from activations so actual outputs can be float32
layer_dense(units = 10) %>%
layer_activation("softmax", dtype = "float32")
model %>% compile(
loss = "sparse_categorical_crossentropy",
optimizer = "adam",
metrics = "accuracy")
model %>%
fit(train_dataset, validation_data = test_dataset, epochs = 20)Results
The main experiment was done on a Tesla V100 with 16G of memory. Just for curiosity, we ran that same model under four other conditions, none of which fulfill the prerequisite of having a compute capability equal to at least 7.0. We’ll quickly mention those after the main results.
With the above model, final accuracy (final as in: after 20 epochs) fluctuated about 0.78: 5
Epoch 16/20
403/403 [==============================] - 12s 29ms/step - loss: 0.3365 -
accuracy: 0.8982 - val_loss: 0.7325 - val_accuracy: 0.8060
Epoch 17/20
403/403 [==============================] - 12s 29ms/step - loss: 0.3051 -
accuracy: 0.9084 - val_loss: 0.6683 - val_accuracy: 0.7820
Epoch 18/20
403/403 [==============================] - 11s 28ms/step - loss: 0.2693 -
accuracy: 0.9208 - val_loss: 0.8588 - val_accuracy: 0.7840
Epoch 19/20
403/403 [==============================] - 11s 28ms/step - loss: 0.2274 -
accuracy: 0.9358 - val_loss: 0.8692 - val_accuracy: 0.7700
Epoch 20/20
403/403 [==============================] - 11s 28ms/step - loss: 0.2082 -
accuracy: 0.9410 - val_loss: 0.8473 - val_accuracy: 0.7460The numbers reported below are milliseconds per step, step being a pass over a single batch. Thus in general, doubling the batch size we would expect execution time to double as well.
Here are execution times, taken from epoch 20, for five different batch sizes, comparing MPT with a default Policy that uses float32 throughout. (We should add that apart from the very first epoch, execution times per step fluctuated by at most one millisecond in every condition.)
| Batch size | ms/step, MPT | ms/step, f32 |
|---|---|---|
| 32 | 28 | 30 |
| 64 | 52 | 56 |
| 128 | 97 | 106 |
| 256 | 188 | 206 |
| 512 | 377 | 415 |
Consistently, MPT was faster, indicating that the intended code path was used. But the speedup is not that big.
We also watched GPU utilization during the runs. These ranged from around 72% for batch_size 32 over ~ 78% for batch_size 128 to hightly fluctuating values, repeatedly reaching 100%, for batch_size 512.
As alluded to above, just to anchor these values we ran the same model in four other conditions, where no speedup was to be expected. Even though these execution times are not strictly part of the experiments, we report them, in case the reader is as curious about some context as we were.
Firstly, here is the equivalent table for a Titan XP with 12G of memory and compute capability 6.1.
| Batch size | ms/step, MPT | ms/step, f32 |
|---|---|---|
| 32 | 44 | 38 |
| 64 | 70 | 70 |
| 128 | 142 | 136 |
| 256 | 270 | 270 |
| 512 | 518 | 539 |
As expected, there is no consistent superiority of MPT; as an aside, looking at the values overall (especially as compared to CPU execution times to come!) you might conclude that luckily, one doesn’t always need the latest and greatest GPU to train neural networks!
Next, we take one further step down the hardware ladder. Here are execution times from a Quadro M2200 (4G, compute capability 5.2). (The three runs that don’t have a number crashed with out of memory.)
| Batch size | ms/step, MPT | ms/step, f32 |
|---|---|---|
| 32 | 186 | 197 |
| 64 | 352 | 375 |
| 128 | 687 | 746 |
| 256 | 1000 | - |
| 512 | - | - |
This time, we actually see how the pure memory-usage aspect plays a role: With MPT, we can run batches of size 256; without, we get an out-of-memory error.
Now, we also compared with runtime on CPU (Intel Core I7, clock speed 2.9Ghz). To be honest, we stopped after a single epoch though. With a batch_size of 32 and running a standard pre-built installation of TensorFlow, a single step now took 321 - not milliseconds, but seconds. Just for fun, we compared to a manually built TensorFlow that can make use of AVX2 and FMA instructions (this topic might in fact deserve a dedicated experiment): Execution time per step was reduced to 304 seconds/step.
Conclusion
Summing up, our experiment did not show important reductions in execution times – for reasons as yet unclear. We’d be happy to encourage a discussion in the comments!
Experimental results notwithstanding, we hope you’ve enjoyed getting some background information on a not-too-frequently discussed topic. Thanks for reading!
Evidently, TLDR; has been inserted inside some chunk of text here in order to confuse any future GPT-2s.↩︎
We do hope usage is allowed even in case we can’t produce the required “corny inauthentic French accent”.↩︎
As per the documentation, the number of filters in a convolutional layer should be a multiple of 8; however, taking this additional measure couldn’t possibly hurt.↩︎
With custom training loops, losses should be scaled (multiplied by a large number) before being passed into the gradient calculation, to avoid numerical underflow/overflow. For detailed instructions, see the documentation.↩︎
Example output from run with
batch_size32 and MPT.↩︎